Factorial

The factorial of a positive integer is product of all positive integer less than or equal to 1.  It is denoted by n! where n is a positive integer.  For example,   

 4! = 4 x 3 x 2 x 1 =24 

An older notation for the factorial is 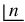.   The notation n! was introduced by Christian Kramp in 1808.

Mathematically, the formula for the factorial is as follows. If n is an integer greater than or equal to 1, then

 n ! = n .( n - 1).( n - 2).( n - 3) ... (3).(2).(1)

The value of 0! is 1. Though it seems to be absurd but for current purpose we just need to memorize it. It helps simplify a lot of equations.

Factorial is used in mathematics particularly in Combinations and Permutations, science and engineering. 

Factorial of fraction (0.8) and negative number (-4.35) is possible but it needs the help advance mathematics like Gamma Function.

 Returns of factorials:

 0!      1 
 1!      1
 2!      2
 3!      6
 4!      24
 5!      120
 6!      720
 7!      5040
 8!      40320
 9!      362880
10!      3628800